Stochastic Optimization

Optimization Algorithms

Optimization forms the basis of machine learning and planning algorithms, e.g., to minimize a loss function or maximize the expected cumulative reward of a sequential problem.

We focus on stochastic optimization based on evolutionary [1] or quantum computing [2] to solve complex problems in planning and (polymatrix) game theory.

Publications:
[1] Productive Fitness
[2] Quantum Annealing for Nash Equilibria Search

Monte Carlo Planning

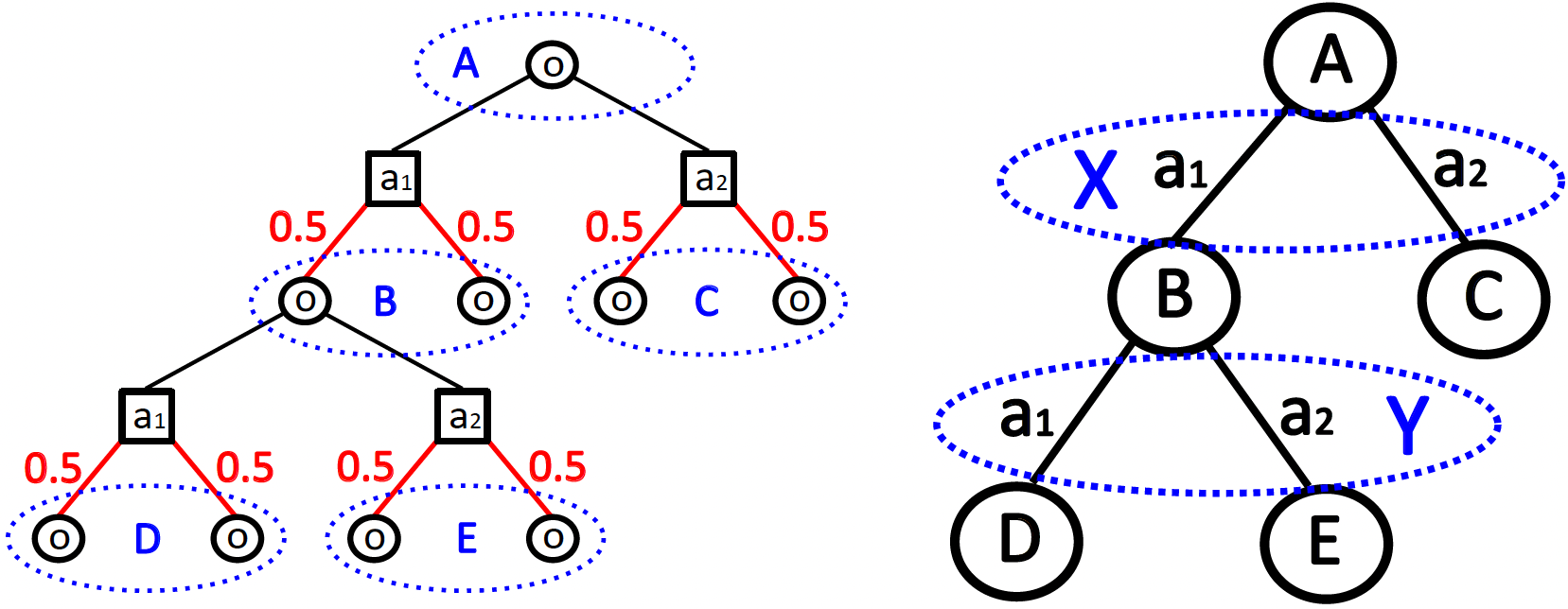
Monte Carlo Planning (MCP) is a sampling-based approach to sequential decision making suitable for domains with enormous branching factors. MCP can be used for online planning, where the agent alternates between acting and reasoning per time step. MCP only requires limited domain knowledge in form of a black box simulator and a computation budget for stochastic optimization of decisions.

We devise algorithms that address various real-world challenges regarding MCP like resource restrictions [1,2] and temporal abstraction [3], and counterfactual reasoning [4]. Our algorithms are open-loop to reduce the search space, while being able to make good decisions in complex domains.

Publications:
[1] Memory Bounded Open-Loop Planning
[2] Adaptive Thompson Sampling Stacks
[3] Subgoal-Based Monte Carlo Planning
[4] Counterfactual Monte Carlo Planning